Differential Calculus of the Female Body: the P”Z point
Ever since the Renaissance, savants and artists have tried to apply rational thought on the problems of defining beauty. Golden ratio, Vitruvian Man, you name it. Some attempts have been made also to enumerate (and name, in a progressively ridiculous way) the “sexiest” points on the female body. (The arithmetic analysis of female nature is beyond the scope of this article). Here we present a modern take on the problem, applying simple calculus techniques.
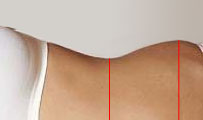
A traditional modern (oxymoron not intended) measure of “sexyness” of the female body is the waist-to-hip ratio (WHR), obtained by dividing the circumference of the waist with that of the hip (“ideal” value is supposed to be 0.7). WHR is inherent in the currently used unscientific notation (i.e. 90-60-90).
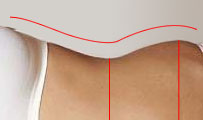
Assuming that the cross-section of the body in these two points is an ellipsoidal curve with a constant eccentricity (width/height ratio), we can get rid of the extra dimension and instead of the circumference use the visual width of the torso. We talk about width, i.e. size when standing up, as the body takes a non-symmetric shape when lying on its side. For ease of presentation, we will depict the upright body in a 90 degree widdershins rotation so we can view the curvature as an algebraic function (with the zero point at the central line of the body — the one that passes throught the nose and the navel). The waistline and the hipline are the local min and max points of the curve.
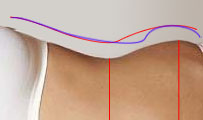
Looking at it this way it is easily seen why WHR is not an adequate measure. Have a look for example at this other function (blue line) with the same min and max values (i.e. same ‘waist’ and ‘hip’ measures), but with a significally different “sexyness”. Therefore, we need another measure to add, so we can unequivocally define the exact shape of the pelvic region.
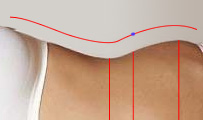
Intuitively, we feel that the important thing to measure should be related to the angle of the body curve (an angle of a curve in a point is defined as the angle of the tangent in that point). A natural choice of such a point is the zero of the second derivative of the curve (the zeroes of the first derivative we already have - these are the min and max values). The zero point of the second derivative is the place where the curve stops being concave and flexes towards convexity (or vice versa) - here marked by the blue spot.
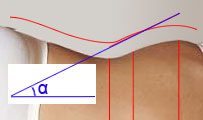
The angle of the tangent in that point (i.e. the value of the first derivative in the point where the second derivative is zero) gives us a better measure of sexyness (well, maybe we’ll need the min and max values too). Going back to the blue curve two paragraphs above, we can see that the tangent to that curve in the zero of the second derivative will be much steeper, even though the min and max values are the same.
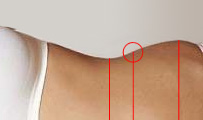
The said point is thus another important “sexy” point (as well as the points on the hip and waist), and I hereby name it the P”Z-point (P[elvic]“[second derivative]Z[ero] - point). Likewise we also have P’Zmin and P’Zmax points, which are used in the already popular waist and hip measures.
As a preliminary result of this article, we propose that female proportions are noted as a four-dimensional vector <x0, x1, x2, x3>, where x0, x1 and x3 are the familiar breast, waist and hip measures, while x2 is the angle α, in radians. In a non-formal manner we can write x0-x1-x2-x3 (i.e. 90-60-0.56-90, instead of the non-specific 90-60-90). We also post as an open problem in front of the scientific community the matter of defining in a better way the shape of the female breast.